Worked example 10.5: Rod supported by a strut

Question: A uniform horizontal rod of mass $m=15 {\rm kg}$ is attached to a vertical wall at one end, and is supported, from below, by a light rigid strut at the other. The strut is attached to the rod at one end, and the wall at the other, and subtends an angle of $\theta = 30^\circ$ with the rod. Find the horizontal and vertical reactions at the point where the strut is attached to the rod, and the points where the rod and the strut are attached to the wall.

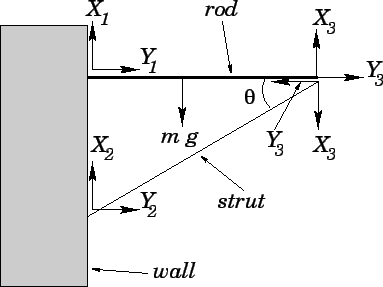
Answer: Let us call the vertical reactions at the joints $X_1$, $X_2$, and $X_3$. Let the corresponding horizontal reactions be $Y_1$, $Y_2$, and $Y_3$. See the diagram. Here, we have made use of the fact that the strut and the rod exert equal and opposite reactions on one another, in accordance with Newton's third law. Setting the net vertical force on the rod to zero yields

$$X_1 + X_3 - m g = 0.$$

Setting the net horizontal force on the rod to zero gives

$$Y_1+Y_3 = 0.$$

Setting the net vertical force on the strut to zero yields

$$X_2-X_3=0.$$

Finally, setting the net horizontal force on the strut to zero yields

$$Y_2-Y_3 = 0.$$

The above equations can be solved to give

$$-Y_1 = Y_2= Y_3 = Y,$$

and

$$X_2 = X_3 = X,$$

with

$$X_1 = m g -X.$$

There now remain only two unknowns, $X$ and $Y$.

Setting the net torque acting on the rod about the point where it is connected to the wall to zero, we obtain

$$m g l/2 - X_3 l =0,$$

where $l$ is the length of the rod. Here, we have used the fact that the centre of gravity of the rod lies at its mid-point. The above equation implies that

$$X_3 = X = m g/2= 15\times 9.81/2 = 73.58 {\rm N}.$$

We also have $X_1=m g-X = 73.58 {\rm N}$. Setting the net torque acting on the strut about the point where it is connected to the wall to zero, we find

$$Y_3 h \sin\theta - X_3 h \cos\theta = 0,$$

where $h$ is the length of the strut. Thus,

$$Y_3 = Y = \frac{X}{\tan \theta} = \frac{73.58}{\tan 30^\circ} =127.44 {\rm N}.$$

In summary, the vertical reactions are $X_1=X_2=X_3= 73.58 {\rm N}$, and the horizontal reactions are $-Y_1=Y_2=Y_3=127.44 {\rm N}.$