


Next: Equilibrium of a laminar
Up: Statics
Previous: Introduction
Consider a general extended body which is subject to a number of external forces.
Let us model this body as a swarm of 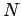 point particles. In the limit that
point particles. In the limit that
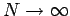 , this model becomes a fully accurate representation of the body's
dynamics.
, this model becomes a fully accurate representation of the body's
dynamics.
In Sect. 6.3 we determined that the overall translational equation
of motion of a general 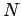 -component system can
be written in the form
-component system can
be written in the form
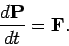 |
(456) |
Here,  is the total linear momentum of the system, and
is the total linear momentum of the system, and
 |
(457) |
is the resultant of all the external forces acting on the system. Note that 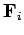 is the external force acting on the
is the external force acting on the  th component of the system.
th component of the system.
Equation (456) effectively determines the translational motion of the system's centre of mass.
Note, however, that in order to fully determine the motion of the system we must also follow its
rotational motion about its centre of mass (or any other convenient reference point).
In Sect. 9.4 we determined that the overall rotational equation of motion
of a general 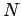 -component system (with central internal forces) can
be written in the form
-component system (with central internal forces) can
be written in the form
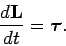 |
(458) |
Here, 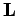 is the total angular momentum of the system (about the origin of
our coordinate scheme), and
is the total angular momentum of the system (about the origin of
our coordinate scheme), and
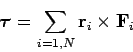 |
(459) |
is the resultant of all the external torques acting on the system (about the
origin of our coordinate scheme). In the above, 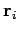 is the vector
displacement of the
is the vector
displacement of the  th component of the system.
th component of the system.
What conditions must be satisfied by the various external forces and torques acting
on the system if it is to remain stationary in time? Well,
if the system does not evolve in time then its net linear momentum,  ,
and its net angular momentum,
,
and its net angular momentum, 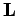 , must both remain constant.
In other words,
, must both remain constant.
In other words,
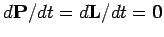 .
It
follows from Eqs. (456) and (458) that
.
It
follows from Eqs. (456) and (458) that
In other words, the net external force acting on system must be zero, and the
net external torque acting on the system must be zero. To be more exact:
The components of the net external force acting along any three independent directions
must all be zero;
and
The magnitudes of the net external torques acting about any three independent axes
(passing through the origin of the coordinate system) must all be zero.
In a nutshell,
these are the principles of statics.
It is clear that the above principles are necessary conditions for a general physical
system not to evolve in time. But, are they also sufficient conditions? In other
words, is it necessarily true that a general system which satisfies these conditions does not
exhibit any time variation? The answer to this question is as follows: if the
system under investigation is a rigid body, such that the motion of any
component of the body necessarily implies the motion of the whole body, then the
above principles are necessary and sufficient conditions for the existence of an equilibrium
state. On the other hand, if the system is not a rigid body, so
that some components of the body can move independently of others, then
the above conditions only guarantee that the system remains static in an average
sense.
Before we attempt to apply the principles of statics, there are a couple
of important points which need clarification. Firstly, does it matter about
which point we calculate the net torque acting on the system? To be more
exact, if we determine that the net torque acting about a given point
is zero does this necessarily imply that the net torque acting about any
other point is also zero? Well,
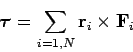 |
(462) |
is the net torque acting on the system about the origin of our coordinate scheme.
The net torque about some general point 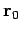 is simply
is simply
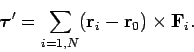 |
(463) |
However, we can rewrite the above expression as
 |
(464) |
Now, if the system is in equilibrium then
 . Hence, it follows
from the above equation that
. Hence, it follows
from the above equation that
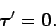 |
(465) |
In other words, for a system in equilibrium, the determination that the net torque acting
about a given point is zero necessarily implies that the net torque acting about
any other point is also zero. Hence, we can choose the point about which we calculate the
net torque at will--this choice is usually made so as to simplify the calculation.
Another question which needs clarification is as follows. At which point should
we assume that the weight of the system acts in order to calculate the contribution
of the weight to the net torque acting about a given point? Actually, in Sect. 8.11,
we effectively answered this question by assuming that the weight
acts at the centre of mass of the system. Let
us now justify this assumption. The external force acting on the  th component
of the system due to its weight is
th component
of the system due to its weight is
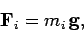 |
(466) |
where 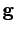 is the acceleration due to gravity (which is assumed to be uniform
throughout the system). Hence, the net gravitational torque acting on the system about the
origin of our coordinate scheme is
is the acceleration due to gravity (which is assumed to be uniform
throughout the system). Hence, the net gravitational torque acting on the system about the
origin of our coordinate scheme is
 |
(467) |
where
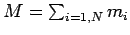 is the total mass of the system, and
is the total mass of the system, and
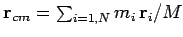 is the position vector of its centre of mass.
It follows, from the above equation, that the net gravitational torque acting on the system
about a given point can be calculated by assuming that the total mass of the system is
concentrated at its centre of mass.
is the position vector of its centre of mass.
It follows, from the above equation, that the net gravitational torque acting on the system
about a given point can be calculated by assuming that the total mass of the system is
concentrated at its centre of mass.



Next: Equilibrium of a laminar
Up: Statics
Previous: Introduction
Richard Fitzpatrick
2006-02-02
![]() -component system can
be written in the form
-component system can
be written in the form

![]() -component system (with central internal forces) can
be written in the form
-component system (with central internal forces) can
be written in the form
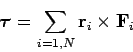
![]() ,
and its net angular momentum,
,
and its net angular momentum, ![]() , must both remain constant.
In other words,
, must both remain constant.
In other words,
![]() .
It
follows from Eqs. (456) and (458) that
.
It
follows from Eqs. (456) and (458) that
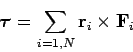
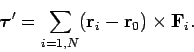

![]() th component
of the system due to its weight is
th component
of the system due to its weight is
