Worked example 9.2: Angular momentum of a sphere

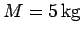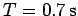Question: A uniform sphere of mass $M=5 {\rm kg}$ and radius $a=0.2 {\rm m}$ spins about an axis passing through its centre with period $T=0.7 {\rm s}$. What is the angular momentum of the sphere?

Answer: The angular velocity of the sphere is

$$\omega = \frac{2 \pi}{T} = \frac{2 \pi}{0.7}= 8.98 {\rm rad./s}.$$

The moment of inertia of the sphere is

$$I = \frac{2}{5} M a^2 = 0.4\times 5\times(0.2)^2 = 0.08 {\rm kg m^2}.$$

Hence, the angular momentum of the sphere is

$$L = I \omega = 0.08\times 8.98 = 0.718 {\rm kg m^2/s}.$$