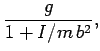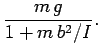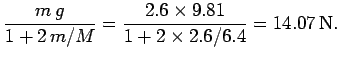Next: Worked example 8.5: Hinged
Up: Rotational motion
Previous: Worked example 8.3: Moment
Question: A weight of mass
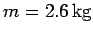 is suspended via
a light inextensible cable which is wound around a pulley of mass
is suspended via
a light inextensible cable which is wound around a pulley of mass
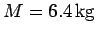 and radius
and radius
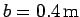 . Treating the pulley as a uniform disk, find the downward
acceleration of the weight and the tension in the cable. Assume that the cable
does not slip with respect to the pulley.
. Treating the pulley as a uniform disk, find the downward
acceleration of the weight and the tension in the cable. Assume that the cable
does not slip with respect to the pulley.
Answer: Let  be the instantaneous downward velocity of the weight,
be the instantaneous downward velocity of the weight,  the
instantaneous angular velocity of the pulley, and
the
instantaneous angular velocity of the pulley, and 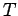 the tension in the cable.
Applying Newton's second law to the vertical motion of the weight, we obtain
the tension in the cable.
Applying Newton's second law to the vertical motion of the weight, we obtain
The angular equation of motion of the pulley is written
where 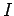 is its moment of inertia, and
is its moment of inertia, and 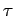 is the torque acting
on the pulley. Now, the only force acting on the pulley (whose
line of action does not pass through the pulley's axis of rotation) is the tension in the cable. The
torque associated with this force is the product of the tension,
is the torque acting
on the pulley. Now, the only force acting on the pulley (whose
line of action does not pass through the pulley's axis of rotation) is the tension in the cable. The
torque associated with this force is the product of the tension, 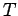 , and the perpendicular
distance from the line of action of this force to the rotation axis, which is equal to the
radius,
, and the perpendicular
distance from the line of action of this force to the rotation axis, which is equal to the
radius, 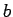 , of the pulley. Hence,
, of the pulley. Hence,
If the cable does not slip with respect to the pulley, then its
downward velocity,  , must match the tangential velocity of the outer surface of the
pulley,
, must match the tangential velocity of the outer surface of the
pulley, 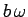 . Thus,
. Thus,
It follows that
The above equations can be combined to give
Now, the moment of inertia of the pulley is
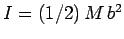 . Hence,
the above expressions reduce to
. Hence,
the above expressions reduce to



Next: Worked example 8.5: Hinged
Up: Rotational motion
Previous: Worked example 8.3: Moment
Richard Fitzpatrick
2006-02-02


![]() be the instantaneous downward velocity of the weight,
be the instantaneous downward velocity of the weight, ![]() the
instantaneous angular velocity of the pulley, and
the
instantaneous angular velocity of the pulley, and ![]() the tension in the cable.
Applying Newton's second law to the vertical motion of the weight, we obtain
the tension in the cable.
Applying Newton's second law to the vertical motion of the weight, we obtain