


Next: Example Syzygy Calculations
Up: Lunar-Solar Syzygies and Eclipses
Previous: Introduction
We can determine the lunar-solar elongation by combining the solar and
lunar models described in the previous two chapters. Our elongation model is as
follows:
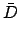 |
 |
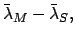 |
(133) |
 |
 |
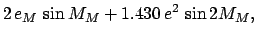 |
(134) |
 |
 |
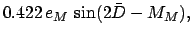 |
(135) |
 |
 |
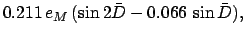 |
(136) |
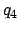 |
 |
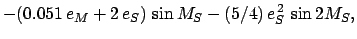 |
(137) |
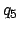 |
 |
 |
(138) |
 |
 |
 |
(139) |
Here, 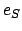 ,
, 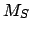 , and
, and
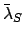 are the eccentricity, mean anomaly, and mean longitude of the sun's apparent orbit about the earth, respectively. Moreover,
are the eccentricity, mean anomaly, and mean longitude of the sun's apparent orbit about the earth, respectively. Moreover, 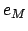 ,
,
 ,
,
 , and
, and 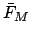 are the eccentricity,
mean anomaly, mean longitude, and mean argument of latitude of
the moon's orbit, respectively.
are the eccentricity,
mean anomaly, mean longitude, and mean argument of latitude of
the moon's orbit, respectively.
The lunar-solar elongation can be calculated with the aid of Tables 40 and 41.
Table 40 allows the mean lunar-solar elongation, 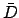 , the mean lunar
argument of latitude,
, the mean lunar
argument of latitude, 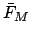 , the mean anomaly of the sun,
, the mean anomaly of the sun, 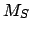 ,
and the mean anomaly of the moon,
,
and the mean anomaly of the moon,  , to be determined as functions of time.
Table 41 specifies the anomalies
, to be determined as functions of time.
Table 41 specifies the anomalies 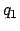 -
-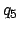 as functions of their
various arguments.
as functions of their
various arguments.
The procedure for using the tables is as follows:
- Determine the fractional Julian day number,
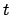 , corresponding to the date and time
at which the lunar-solar elongation is to be calculated with the aid of Tables 27-29. Form
, corresponding to the date and time
at which the lunar-solar elongation is to be calculated with the aid of Tables 27-29. Form
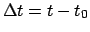 , where
, where
 is the epoch.
is the epoch.
- Enter Table 40 with the digit for each power of 10
in
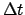 and take out the corresponding values of
and take out the corresponding values of
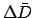 ,
,
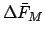 ,
,
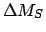 , and
, and  . If
. If 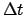 is negative then the
values are minus those shown in the table.
The value of the mean lunar-solar elongation,
is negative then the
values are minus those shown in the table.
The value of the mean lunar-solar elongation, 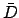 , is the
sum of all the
, is the
sum of all the 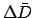 values plus the value of
values plus the value of 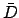 at the epoch.
Likewise, the value of the mean lunar argument of latitude,
at the epoch.
Likewise, the value of the mean lunar argument of latitude, 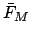 , is the
sum of all the
, is the
sum of all the
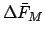 values plus the value of
values plus the value of 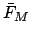 at the epoch. Moreover, the value of the solar mean anomaly,
at the epoch. Moreover, the value of the solar mean anomaly, 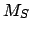 , is
the sum of all the
, is
the sum of all the 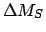 values plus the value of
values plus the value of 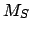 at the epoch. Finally, the value
of the lunar mean anomaly,
at the epoch. Finally, the value
of the lunar mean anomaly,  , is the
sum of all the
, is the
sum of all the  values plus the value of
values plus the value of  at the epoch.
Add as many multiples of
at the epoch.
Add as many multiples of  to
to 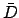 ,
, 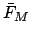 ,
, 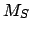 , and
, and  as is required to make them all fall in the range
as is required to make them all fall in the range 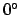 to
to  .
.
- Form the five arguments
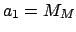 ,
,
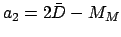 ,
, 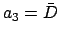 ,
, 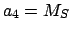 ,
,
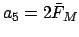 . Add as
many multiples of
. Add as
many multiples of  to the arguments as is required to make them all fall in the range
to the arguments as is required to make them all fall in the range
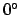 to
to  . Round each argument to the nearest degree.
. Round each argument to the nearest degree.
- Enter Table 41 with the value of each of the five arguments
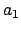 -
- and take out the
value of each of the five corresponding anomalies
and take out the
value of each of the five corresponding anomalies 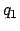 -
-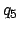 . It is necessary to interpolate if the arguments are odd.
. It is necessary to interpolate if the arguments are odd.
- The lunar-solar elongation is given by
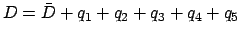 .
If necessary, convert
.
If necessary, convert 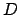 into an angle in the range
into an angle in the range 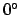 to
to  .
The decimal fraction can be converted into arc minutes
using Table 31.
.
The decimal fraction can be converted into arc minutes
using Table 31.
In order to facilitate the calculation of syzygies, the above model has been used to contruct Table 42, which lists
the dates and fractional Julian day numbers of the first new moons of the years 1900-2099 CE. Two examples
of syzygy calculations are given below.



Next: Example Syzygy Calculations
Up: Lunar-Solar Syzygies and Eclipses
Previous: Introduction
Richard Fitzpatrick
2010-07-21
![]() , the mean lunar
argument of latitude,
, the mean lunar
argument of latitude, ![]() , the mean anomaly of the sun,
, the mean anomaly of the sun, ![]() ,
and the mean anomaly of the moon,
,
and the mean anomaly of the moon, ![]() , to be determined as functions of time.
Table 41 specifies the anomalies
, to be determined as functions of time.
Table 41 specifies the anomalies ![]() -
-![]() as functions of their
various arguments.
as functions of their
various arguments.