


Next: Example Longitude Calculations
Up: The Moon
Previous: The Moon
The orbit of the moon around the earth is strongly perturbed by the
gravitational influence of the sun. It follows that we cannot derive an accurate lunar longitude model
from Keplerian orbit theory alone. Instead, we shall employ a
greatly simplified version of modern lunar theory. According to such
theory, the time variation of the ecliptic longitude of the moon is fairly
well represented by the following
formulae (see http://jgiesen.de/moonmotion/index.html, or Astronomical Algorithms, J. Meeus, Willmann-Bell, 1998):
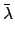 |
 |
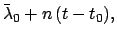 |
(114) |
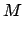 |
 |
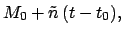 |
(115) |
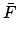 |
 |
 |
(116) |
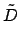 |
 |
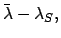 |
(117) |
 |
 |
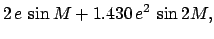 |
(118) |
 |
 |
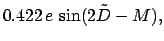 |
(119) |
 |
 |
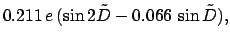 |
(120) |
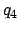 |
 |
 |
(121) |
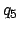 |
 |
 |
(122) |
 |
 |
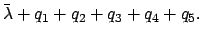 |
(123) |
Here, 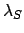 and
and 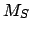 are the longitude and mean anomaly
of the sun, respectively. Moreover,
are the longitude and mean anomaly
of the sun, respectively. Moreover, 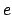 ,
, 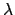 ,
, 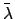 ,
, 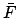 ,
and
,
and 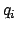 are the eccentricity, longitude, mean longitude, mean argument of latitude,
and
are the eccentricity, longitude, mean longitude, mean argument of latitude,
and 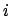 th anomaly of the moon, respectively. The moon's first anomaly
is due to the eccentricity of its orbit, and is very similar in form to that obtained from Keplerian orbit theory (see Cha. 4). The
moon's second, third, and fourth anomalies are knows as
evection, variation, and the annual inequality, respectively, and originate from
the perturbing influence of the sun. Finally, the moon's fifth anomaly is
called the reduction to the ecliptic, and is a consequence of the fact that the moon's
orbit is slightly tilted with respect to the plane of the ecliptic.
Note that Ptolemy's lunar theory only takes the first two
lunar anomalies into account.
The moon's orbital elements--
th anomaly of the moon, respectively. The moon's first anomaly
is due to the eccentricity of its orbit, and is very similar in form to that obtained from Keplerian orbit theory (see Cha. 4). The
moon's second, third, and fourth anomalies are knows as
evection, variation, and the annual inequality, respectively, and originate from
the perturbing influence of the sun. Finally, the moon's fifth anomaly is
called the reduction to the ecliptic, and is a consequence of the fact that the moon's
orbit is slightly tilted with respect to the plane of the ecliptic.
Note that Ptolemy's lunar theory only takes the first two
lunar anomalies into account.
The moon's orbital elements--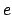 ,
, 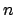 ,
,  ,
,  ,
,
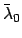 ,
, 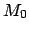 , and
, and 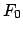 --for the J2000 epoch are listed in Table 35. Note that the lunar perigee precesses in the
direction of the moon's orbital motion at the rate of
--for the J2000 epoch are listed in Table 35. Note that the lunar perigee precesses in the
direction of the moon's orbital motion at the rate of
 per day, or
per day, or  in 8.85 years. This
very large precession rate (more than 2000 times the corresponding
precession rate for the sun's apparent orbit) is another consequence of the strong
perturbing influence of the sun on the moon's orbit.
The above formulae are capable of matching NASA ephemeris
data during the years 1995-2006 CE with a mean error of
in 8.85 years. This
very large precession rate (more than 2000 times the corresponding
precession rate for the sun's apparent orbit) is another consequence of the strong
perturbing influence of the sun on the moon's orbit.
The above formulae are capable of matching NASA ephemeris
data during the years 1995-2006 CE with a mean error of 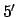 and
a maximum error of
and
a maximum error of 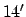 .
.
The ecliptic longitude of the moon can be calculated with the aid of Tables 36 and 37.
Table 36 allows the lunar mean longitude, 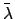 , mean anomaly,
, mean anomaly, 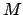 , and mean argument of latitude,
, and mean argument of latitude, 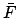 , to be determined as functions of time.
Table 37 specifies the lunar anomalies,
, to be determined as functions of time.
Table 37 specifies the lunar anomalies, 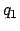 -
-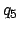 , as functions of their various arguments.
, as functions of their various arguments.
The procedure for using the tables is as follows:
- Determine the fractional Julian day number,
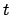 , corresponding to the date and time
at which the moon's ecliptic longitude is to be calculated with the aid of Tables 27-29. Form
, corresponding to the date and time
at which the moon's ecliptic longitude is to be calculated with the aid of Tables 27-29. Form
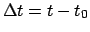 , where
, where
 is the epoch.
is the epoch.
- Calculate the ecliptic longitude,
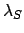 , and the mean anomaly,
, and the mean anomaly, 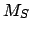 , of the
sun using the procedure set out in Sect. 5.1.
, of the
sun using the procedure set out in Sect. 5.1.
- Enter Table 36 with the digit for each power of 10
in
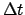 and take out the corresponding values of
and take out the corresponding values of
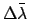 ,
, 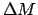 ,
and
,
and 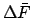 . If
. If 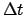 is negative then the
values are minus those shown in the table.
The value of the mean longitude,
is negative then the
values are minus those shown in the table.
The value of the mean longitude, 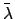 , is the
sum of all the
, is the
sum of all the
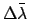 values plus the value of
values plus the value of 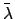 at the epoch. Likewise, the value of the mean anomaly,
at the epoch. Likewise, the value of the mean anomaly, 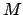 , is
the sum of all the
, is
the sum of all the 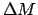 values plus the value of
values plus the value of 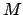 at the epoch. Finally, the value of the mean argument of latitude,
at the epoch. Finally, the value of the mean argument of latitude, 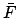 , is the
sum of all the
, is the
sum of all the 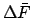 values plus the value of
values plus the value of 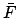 at the epoch.
Add as many multiples of
at the epoch.
Add as many multiples of  to
to 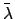 ,
, 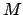 , and
, and 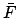 as is required to make them all fall in the range
as is required to make them all fall in the range 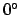 to
to  .
.
- Form
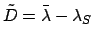 .
.
- Form the five arguments
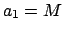 ,
,
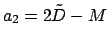 ,
, 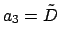 ,
, 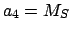 ,
, 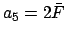 . Add as
many multiples of
. Add as
many multiples of  to the arguments as is required to make them all fall in the range
to the arguments as is required to make them all fall in the range
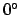 to
to  . Round each argument to the nearest degree.
. Round each argument to the nearest degree.
- Enter Table 37 with the value of each of the five arguments
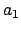 -
- and take out the
value of each of the five corresponding anomalies
and take out the
value of each of the five corresponding anomalies 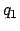 -
-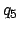 . It is necessary to interpolate if the arguments are odd.
. It is necessary to interpolate if the arguments are odd.
- The moon's ecliptic longitude is given by
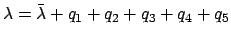 .
If necessary, convert
.
If necessary, convert 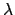 into an angle in the range
into an angle in the range 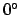 to
to  .
The decimal fraction can be converted into arc minutes
using Table 31. Round to the nearest arc minute.
.
The decimal fraction can be converted into arc minutes
using Table 31. Round to the nearest arc minute.
Two examples of the use of this procedure are given below.



Next: Example Longitude Calculations
Up: The Moon
Previous: The Moon
Richard Fitzpatrick
2010-07-21
![]() , mean anomaly,
, mean anomaly, ![]() , and mean argument of latitude,
, and mean argument of latitude, ![]() , to be determined as functions of time.
Table 37 specifies the lunar anomalies,
, to be determined as functions of time.
Table 37 specifies the lunar anomalies, ![]() -
-![]() , as functions of their various arguments.
, as functions of their various arguments.