


Next: Equation of Time
Up: The Sun
Previous: Example Longitude Calculations
We can also use Tables 32 and 33 to calculate the dates of the equinoxes and solstices,
and, hence, the lengths of the seasons, in a given year. The vernal equinox (i.e., the point on the sun's apparent orbit at which it passes through the celestial equator
from south to north)
corresponds to
 , the summer solstice (i.e., the
point at which the sun is furthest north of the celestial equator) to
, the summer solstice (i.e., the
point at which the sun is furthest north of the celestial equator) to
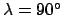 , the autumnal equinox (i.e., the point at which the
sun passes through the celestial equator from north to south) to
, the autumnal equinox (i.e., the point at which the
sun passes through the celestial equator from north to south) to
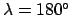 , and the
winter solstice (i.e., the point at which the sun is furthest south of the celestial equator) to
, and the
winter solstice (i.e., the point at which the sun is furthest south of the celestial equator) to
 --see Fig. 22. Furthermore, spring is defined as the period between the spring
equinox and the summer solstice, summer as the period between the summer solstice and
the autumnal equinox, autumn as the period between the autumnal equinox and the
winter solstice, and winter as the period between the winter solstice and the following
vernal equinox. Consider the year 2000 CE.
For the case of the vernal equinox, we can
first estimate the
time at which this event takes place by approximating the solar
longitude as the mean
solar longitude: i.e.,
--see Fig. 22. Furthermore, spring is defined as the period between the spring
equinox and the summer solstice, summer as the period between the summer solstice and
the autumnal equinox, autumn as the period between the autumnal equinox and the
winter solstice, and winter as the period between the winter solstice and the following
vernal equinox. Consider the year 2000 CE.
For the case of the vernal equinox, we can
first estimate the
time at which this event takes place by approximating the solar
longitude as the mean
solar longitude: i.e.,
We obtain
Calculating the true solar longitude at this time, using Tables 32 and 33, we get
 Now, the actual vernal equinox occurs
when
Now, the actual vernal equinox occurs
when
 .
Thus, a much better estimate for the date of the vernal equinox
is
.
Thus, a much better estimate for the date of the vernal equinox
is
which
corresponds to 7:00 UT on March 20. Similar calculations show that the summer solstice takes place at
corresponding to 2:00 UT on June 21, that the autumnal equinox
takes place at
corresponding to 17:00 UT
on September 22, and that the winter solstice takes place at
corresponding to 14:00 UT on December 21.
Thus, the length of spring is  days,
the length of summer
days,
the length of summer  days,
and the length of autumn
days,
and the length of autumn 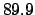 days.
Finally, the length of winter is the length
of the tropical year (i.e., the time period between successive vernal equinoxes), which is
days.
Finally, the length of winter is the length
of the tropical year (i.e., the time period between successive vernal equinoxes), which is
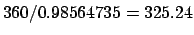 days, minus the sum of the lengths of the
other three seasons. This gives
days, minus the sum of the lengths of the
other three seasons. This gives  days.
days.
Figure 22:
The sun's apparent orbit around the earth, 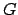 , showing the vernal equinox (VE), summer
solstice (SS), autumnal equinox (AE), and winter solstice (WS). Here,
, showing the vernal equinox (VE), summer
solstice (SS), autumnal equinox (AE), and winter solstice (WS). Here, 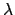 ,
, 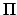 ,
, 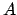 , and
, and  are the ecliptic longitude, perigee, apogee, and geometric center of the orbit, respectively. The lengths
of the seasons (in days) are indicated.
are the ecliptic longitude, perigee, apogee, and geometric center of the orbit, respectively. The lengths
of the seasons (in days) are indicated.
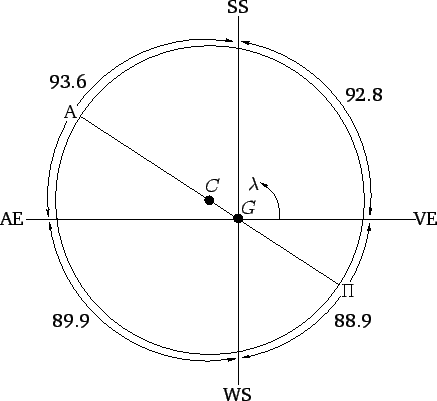 |
Figure 22 illustrates the relationship between the equinox and solstice points, and the
lengths of the seasons. The earth is displaced from the geometric center of the sun's apparent orbit in the direction of
the solar perigee, which presently lies between the winter solstice and the vernal equinox. This displacement (which is
greatly exaggerated in the figure) has
two effects. Firstly, it causes the arc of the sun's apparent orbit between the summer solstice and autumnal equinox
to be longer than that between the winter solstice and the vernal equinox. Secondly, it causes the
sun to appear to move faster in winter than in summer, in accordance with Kepler's second law, since the sun is closer to the earth in the
former season. Both of these effects tend to lengthen summer, and
shorten winter. Hence, summer is presently the longest season, and winter the shortest.



Next: Equation of Time
Up: The Sun
Previous: Example Longitude Calculations
Richard Fitzpatrick
2010-07-21
