

Next: Model of Ptolemy
Up: Geometric Planetary Orbit Models
Previous: Model of Kepler
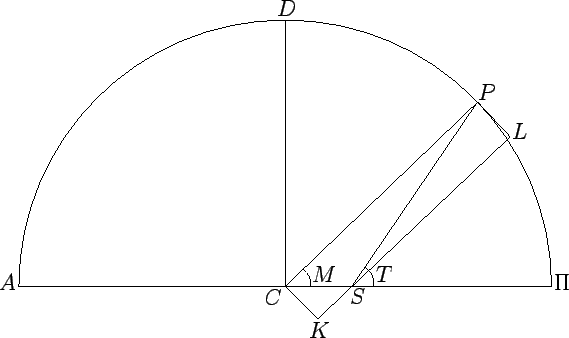
Hipparchus' geometric model of the apparent orbit of the sun around the earth can also be used to describe a heliocentric planetary orbit. The model is illustrated in Fig. 18. The orbit of the planet corresponds
to the circle 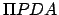 (only half of which is shown), where
(only half of which is shown), where 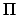 is the perihelion point,
is the perihelion point, 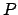 the planet's instantaneous position,
and
the planet's instantaneous position,
and 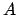 the aphelion point. The diameter
the aphelion point. The diameter 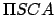 is the effective major axis of the orbit (to be more exact, it
is the line of apsides), where
is the effective major axis of the orbit (to be more exact, it
is the line of apsides), where 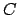 is the geometric center of circle
is the geometric center of circle 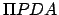 , and
, and 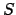 the fixed position of the sun.
The radius
the fixed position of the sun.
The radius 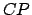 of circle
of circle 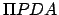 is the effective major radius,
is the effective major radius, 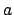 , of the orbit. The distance
, of the orbit. The distance 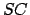 is
equal to
is
equal to 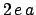 , where
, where 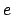 is the orbit's effective eccentricity. The angle
is the orbit's effective eccentricity. The angle 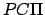 is identified with the mean anomaly,
is identified with the mean anomaly, 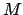 , and increases linearly in time. In other words, as seen from
, and increases linearly in time. In other words, as seen from 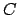 , the planet
, the planet
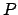 moves uniformly around circle
moves uniformly around circle 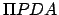 in a counterclockwise direction. Finally,
in a counterclockwise direction. Finally, 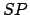 is the radial
distance,
is the radial
distance, 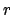 , of the planet from the sun, and angle
, of the planet from the sun, and angle 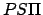 is the planet's true anomaly,
is the planet's true anomaly, 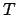 .
.
Figure 18:
A Hipparchian orbit.
 |
Let us draw the straight-line 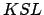 parallel to
parallel to 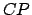 , and passing through point
, and passing through point 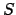 , and then complete the rectangle
, and then complete the rectangle 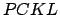 . Simple geometry reveals that
. Simple geometry reveals that
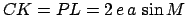 ,
,
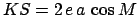 , and
, and
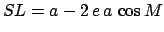 . Moreover,
. Moreover,
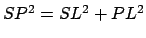 ,
which implies that
,
which implies that
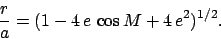 |
(83) |
Now, 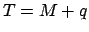 , where
, where 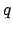 is angle
is angle 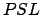 . However,
. However,
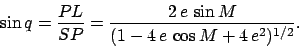 |
(84) |
Finally, expanding the previous two equations to second-order in the small parameter 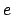 , we obtain
, we obtain
It can be seen, by comparison with Eqs. (81) and (82), that the relative radial distance, 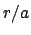 , in the Hipparchian model deviates from that in the (correct) Keplerian model to first-order in
, in the Hipparchian model deviates from that in the (correct) Keplerian model to first-order in 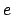 (in fact, the variation of
(in fact, the variation of 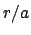 is greater by a factor of
is greater by a factor of 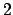 in the former model), whereas
the true anomaly,
in the former model), whereas
the true anomaly, 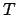 , only deviates to second-order in
, only deviates to second-order in 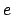 . We conclude that Hipparchus' geometric model
of a heliocentric planetary orbit does a
reasonably good job at predicting the angular position of the planet, relative to the sun, but significantly
exaggerates (by a factor of
. We conclude that Hipparchus' geometric model
of a heliocentric planetary orbit does a
reasonably good job at predicting the angular position of the planet, relative to the sun, but significantly
exaggerates (by a factor of 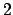 ) the variation in the radial distance between the two during the course of a complete orbital rotation.
) the variation in the radial distance between the two during the course of a complete orbital rotation.


Next: Model of Ptolemy
Up: Geometric Planetary Orbit Models
Previous: Model of Kepler
Richard Fitzpatrick
2010-07-21

![]() parallel to
parallel to ![]() , and passing through point
, and passing through point ![]() , and then complete the rectangle
, and then complete the rectangle ![]() . Simple geometry reveals that
. Simple geometry reveals that
![]() ,
,
![]() , and
, and
![]() . Moreover,
. Moreover,
![]() ,
which implies that
,
which implies that
![]() , we obtain
, we obtain